Leetcode 1235: Maximum Profit in Job Scheduling

https://leetcode.com/problems/maximum-profit-in-job-scheduling/description/

We have n jobs, where every job is scheduled to be done from startTime[i] to endTime[i], obtaining a profit of profit[i].

You're given the startTime , endTime and profit arrays, you need to output the maximum profit you can take such that there are no 2 jobs in the subset with overlapping time range.

If you choose a job that ends at time X you will be able to start another job that starts at time X.

Example 1:

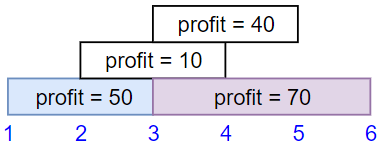
Input: startTime = [1,2,3,3], endTime = [3,4,5,6], profit = [50,10,40,70]
Output: 120
Explanation: The subset chosen is the first and fourth job. 
Time range [1-3]+[3-6] , we get profit of 120 = 50 + 70.

Example 2:

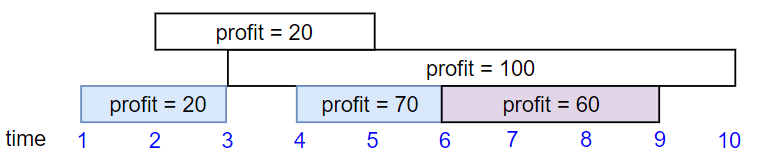
Input: startTime = [1,2,3,4,6], endTime = [3,5,10,6,9], profit = [20,20,100,70,60]
Output: 150
Explanation: The subset chosen is the first, fourth and fifth job. 
Profit obtained 150 = 20 + 70 + 60.

Example 3:

Input: startTime = [1,1,1], endTime = [2,3,4], profit = [5,6,4]
Output: 6

Constraints:

• 1 <= startTime.length == endTime.length == profit.length <= 5 * 10^4
• 1 <= startTime[i] < endTime[i] <= 10^9
• 1 <= profit[i] <= 10^4

Notes:

The first step is that we need to sort the event or job in order.

If we sort them by the starting time, then we need to correlate the starting time with the ending time and profit.

After that, we can run a search using dfs + memorization.

The reason for memorization is to avoid re-calculate the same sub-states.

We will use memo[i] to represent the maximum profit can be gained starting with the ith job.

If we choose the ith job, we have to finish it. So the next available jobs must starts no earlier than the ith job. This gives us the start of the next search.

At current ith job position, do we need to go through all the jobs?

The answer is no. We just need to check all the jobs starting earlier than the end[i]. Why?

The logic is simple: if they start no earlier than the end[i], we just can finish the ith job first, then continue with the following jobs, which is definitely larger than that without choosing the ith job. The profit is always positive.

See the code below:

class Solution {
public:
    int jobScheduling(vector<int>& startTime, vector<int>& endTime, vector<int>& profit) {
        int res = 0, len = startTime.size();
        vector<vector<int>> vs(len);
        for(int i=0; i<len; ++i) vs[i] = {startTime[i], endTime[i], profit[i]};
        sort(vs.begin(), vs.end());
        for(int i=0; i<len; ++i) {
            startTime[i] = vs[i][0];
            endTime[i] = vs[i][1];
            profit[i] = vs[i][2];
        }
        vector<int> memo(len, -1);
        return dfs(startTime, endTime, profit, 0, memo);
    }
private:
    int dfs(vector<int>& ss, vector<int>& es,vector<int>& ps,  int id, vector<int>& memo) {
        if(id <0 || id >= ss.size()) return 0;
        if(memo[id] != -1) return memo[id];
        int t = 0;
        int right = lower_bound(ss.begin(), ss.end(), es[id]) - ss.begin();
     //   cout<<right<<endl;
        for(int i=id; i<right; ++i) {
            int next_id = lower_bound(ss.begin(), ss.end(), es[i]) - ss.begin();
            t = max(t, ps[i] + dfs(ss, es, ps, next_id, memo));
        }
        return memo[id] = t;
    }
};