Leetcode 1183: Maximum Number of Ones

https://leetcode.com/problems/maximum-number-of-ones/description/

Notes:

One of the solution is straightforward: we just need to check both horizontal and vertical directions. If the square sub-matrix can be repeated completely, then it simply repeats all the 1s. So the difficulty part is when there are remainders.

For remainders, we need to consider both directions too. Below is a very good resource on how to deal with the remainders.

https://leetcode.com/problems/maximum-number-of-ones/discuss/377033/C++-O(1)-solution-with-explanation-Totally-intuitive



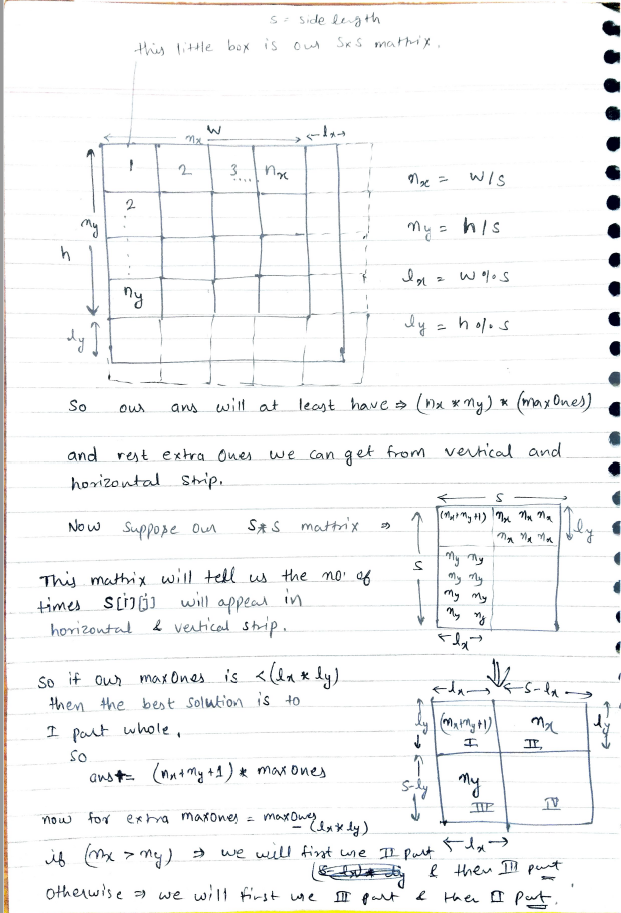
For the remainders partial squares in the two directions, we can essentially "overlap them", as shown in the below figure. The key logic is listed below:

1): If m (the maxOnes) is no larger than lx * ly, we simple place all the 1s in that area, which will give us the maximum number of 1s. And it is (nx + ny + 1) * m;

for example, 10, 10, 4, 4.

then nx = ny = 2; lx=ly = 2. then m = 4 <= lx*ly = 4.

We just need to place the 1s as 2*2. The both vertical and horizontal partial square can repeat all the 1s. And they overlap at the bottom right corner. The overall number is (nx + ny + 1).

2): if m > lx*ly

 After placing 1s in the range I with an area of lx*ly, we still have extra 1s. Now we need to compare nx and ny: how many time are the extra 1s repreated? If nx is larger, we need to place 1s in range II first; otherwise, range III.

3): if we still have extra, we need to place the extra 1s in the unused range (II or III).

4): range IV is never used.


See the code below:

class Solution {
public:
    int maximumNumberOfOnes(int w, int h, int s, int mo) {
        int ans=0, lx=w%s, ly=h%s, nx=w/s, ny=h/s;
        ans=nx*ny*mo;
        if(mo<=lx*ly) ans+=(nx+ny+1)*mo;
        else {
            ans+=(nx+ny+1)*lx*ly;
            mo-=lx*ly;//extra 1s
            if(nx>ny) {
                if(mo<=(s-lx)*ly) ans+=(nx)*mo;
                else {
                    ans+=(s-lx)*ly*(nx);
                    mo-=(s-lx)*ly;//extra 1s
                    ans+=min(mo, (s-ly)*lx )*ny;
                }
            }
            else {
                if(mo<=(s-ly)*lx) ans+=(ny)*mo;
                else {
                    ans+=(s-ly)*lx*(ny);
                    mo-=(s-ly)*lx;//extra 1s
                    ans+=min(mo, (s-lx)*ly )*nx;
                }
            }
        }
        return ans;
    }
};

Another way to think about this question is more abstract:

https://leetcode.com/problems/maximum-number-of-ones/discuss/376911/PythonC++-Solution-with-explanation

"If we create the first square matrix, the big matrix will just be the copies of this one. (translation copies)
The value of each location in the square matrix will appear at multiple locations in the big matrix, count them.
Then assign the ones in the square matrix with more occurrences with 1."

Please see the code below:

class Solution {
public:
    int maximumNumberOfOnes(int width, int height, int sideLength, int maxOnes) {
        int res = 0, w = width, h = height, s = sideLength, m = maxOnes;
        vector<int> ct;
        for(int i=0; i<s; ++i) {
            for(int j=0; j<s; ++j) {
                ct.push_back(((w-i-1)/s + 1)*((h-j-1)/s+1));
            }
        }
        sort(ct.begin(), ct.end(), greater<int>());
        for(int i=0; i<m; ++i) res += ct[i];
        return res;
    }
};

There is another way to implement this idea, which seems easier to understand: we just count the frequency of the occurrence of each position in the square. Then choose the top maxOnes positions to fill with 1, which gives us the most 1s in total.

See the code below:

class Solution {
public:
    int maximumNumberOfOnes(int width, int height, int sideLength, int maxOnes) {
        int res = 0, w = width, h = height, s = sideLength, m = maxOnes;
        vector<int> ct(s*s, 0);
        for(int i=0; i<w; ++i) {
            for(int j=0; j<h; ++j) {
                int id = (i%s)*s + (j%s);
                ++ct[id];
            }
        }
        sort(ct.begin(), ct.end(), greater<int>());
        for(int i=0; i<m; ++i) res += ct[i];
        return res;
    }
};